Affine Transformation

The affine transformation, usually a frequently used term in computer geometry or algebra, has always been an efficient way to record the changes in geometric transformation. The use of t in 3D compression has ever been reported [16].

Ordinary vector algebra uses matrix multiplication to represent linear transformations, and vector addition to represent translations. Using a trick, it is possible to represent both using matrix multiplication. The trick requires that all vectors are augmented with a "1" at the, and all matrices are augmented with an extra row of zeros at the bottom, which is know as the homogeneous coordinates.

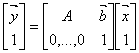                                                                                           (1)

Is equivalent to

If A and b in equation (1) represents the rotation and translation, then the matrix 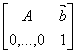 is called the homogeneous transformation matrix from  to .