 |
    |
Efficient k-Support Matrix Pursuit*
Hanjiang Lai1, 3, Yan Pan2, Canyi Lu1, Yong Tang4, and Shuicheng Yan1
1Department of Electrical and Computer Engineering, National University of Singapore, Singapore
laihanj@gmail.com
canyilu@gmail.com
eleyans@nus.edu.sg
2School of Software, Sun Yat-sen University, China
panyan5@mail.sysu.edu.cn
3School of Information Science and Technology, Sun Yat-sen University, China
4School of Computer Science, South China Normal University, China
ytang@scnu.edu.cn
Abstract. In this paper, we study the k-support norm regularized matrix pursuit problem, which is regarded as the core formulation for several popular computer vision tasks. The k-support matrix norm, a convex relaxation of the matrix sparsity combined with the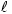 
2-norm penalty, generalizes the recently proposed k-support vector norm. The contributions of this work are two-fold. First, the proposed k-support matrix norm does not suffer from the disadvantages of existing matrix norms towards sparsity and/or low-rankness: 1) too sparse/dense, and/or 2) column independent. Second, we present an efficient procedure for k-support norm optimization, in which the computation of the key proximity operator is substantially accelerated by binary search. Extensive experiments on subspace segmentation, semi-supervised classification and sparse coding well demonstrate the superiority of the new regularizer over existing matrix-norm regularizers, and also the orders-of-magnitude speedup compared with the existing optimization procedure for the k-support norm.
Keywords:
Electronic Supplementary Material:
LNCS 8690, p. 617 ff.
lncs@springer.com
© Springer International Publishing Switzerland 2014